그래프 그리기 06:= 등탄력적 효용함수 그래프 그리기
// 스타타를 이용하여 일반 함수, 즉 y=x , y=x^2 + x + 3 와 같은 함수를 그리고 싶을때
// 오늘은 경제학에서 자주 사용되는 등탄력적 효용함수를 그려보도록 하겠습니다. 이때, 탄력도의 차이에 따른 함수 형태의 차이를 보고자 합니다.
// 그리고 탄력도의 차이에 따른 함수에 따라 소득수준에 따른 한계효용의 변화 역시 비교합니다.
// 등탄력적 효용함수의 일반적 형태...
// 이러한 효용함수의 특징은 소득수준에 따라 탄력도가 항상 ε로 같다는 것입니다.
// 즉, ε값에 따라 그 함수를 그리면 됩니다.
// 함수를 그리는 기본적인 코드는 다음과 같습니다.
twoway (function y = (x^(1-0) - 1)/(1-0), range(0 5)
// ε=0일때, x값 범위를 0과 5로하여 그래프를 그리시오....
// 즉, ε=0일때, 위 함수는 y=x-1이 됩니다...
// 이건 스타타 명령어 줄에서 아무런 자료가 없어도 그려집니다... 위의 function이라는 부분땜시...ㅋ
// 여하튼, ε가 0 , 0.5, 1, 2, 5일때 각 함수를 하나의 그래프로 그리려면....
#delimit ;
twoway (function y = (x^(1-0) - 1)/(1-0), ra(0 5) lcolor(black) lwidth(medium) lpattern(solid))
(function y = (x^(1-0.5) - 1)/(1-0.5), ra(0 5) lcolor(blue) lwidth(medium) lpattern(solid))
(function y = (x^(1-1.1) - 1)/(1-1.1), ra(0.07 5) lcolor(red) lwidth(medium) lpattern(solid))
(function y = (x^(1-2) - 1)/(1-2), ra(0.25 5) lcolor(green) lwidth(medium) lpattern(solid))
(function y = (x^(1-5) - 1)/(1-5), ra(0.52 5) lcolor(green) lwidth(medium) lpattern(dash))
, title("[등탄력도(ε)에 따른 효용함수]")
ytitle("효용(U)") yline(0, lstyle(foreground)) yscale(range(-3 4)) ylabel(-3(1)4, angle(horizontal))
xlabel(1(1)5, tposition(crossing)) xsca(noline)
xtitle("y/μ")
legend(on order(1 "ε=0" 2 "ε=0.5" 3 "ε=1" 4 "ε=2" 5 "ε=5") rows(1)) scheme(sj)
;
#delimit ;
twoway (function y = x^(-0), ra(0 5) lcolor(black) lwidth(medium) lpattern(solid))
(function y = x^(-0.5) , ra(0.057 5) lcolor(blue) lwidth(medium) lpattern(solid))
(function y = x^(-1) , ra(0.23 5) lcolor(red) lwidth(medium) lpattern(solid))
(function y = x^(-2) , ra(0.47 5) lcolor(green) lwidth(medium) lpattern(solid))
(function y = x^(-5) , ra(0.75 5) lcolor(green) lwidth(medium) lpattern(dash))
, title("[등탄력도(ε)에 따른 효용함수의 복지가중치 변화]")
ytitle("한계효용=복지가중치(ΔU)") yline(0, lstyle(foreground)) yscale(range(0 4)) ylabel(0(1)4, angle(horizontal))
xlabel(1(1)5, tposition(crossing)) xsca(noline)
xtitle("y/μ")
legend(on order(1 "ε=0" 2 "ε=0.5" 3 "ε=1" 4 "ε=2" 5 "ε=5") rows(1)) scheme(sj)
;
// 아!! 이게 어떻게 쓰이는 함수냐구요?
// 분야마다 다르겠지만, 경제학에서 사용하는 불평등지수 중 앳킨슨 지수가 있는데, 위 함수는 그 지수를 산출하기 위한 가정한 함수입니다. 여기서 중요한 것은 ε 가 클수록 저소득계층의 한계효용값이 더 크게 나온다는 점입니다. 위의 그림에서 가로축은 평균소득 대비 개인소득의 비율이며, 그래서 1은 개인소득이 평균소득과 같다는 것입니다. 따라서 1보다 작은 부분이 저소득계층을 의미하는 것이고, 예를 들어 0.5의 경우 ε에 따른 한계효용을 비교하면, ε이 클수록 증가하고, 1을 초과하는 상위계층의 경우엔 ε을 크게 가정할수록 한계효용은 더 작게 됩니다. 이러한 한계효용값을 각 개인들의 소득에 대한 가중치로 설정하여, 평균이하 계층의 소득이 낮을수록 평균소득과의 격차가 더 크게 하여, 사회 전체적으로 각 개인들의 소득이 평균소득과 떨어진 거리를 표준화합니다. 표준화한 결과가 바로 앳킨슨 지수입니다.^^ 물론, 이 중간에는 넘 복잡한 수학적 풀이과정이 있어서, 더 자세한 설명을 드리지는 못하겠네요.... 쓰는 사람도 그렇고, 보든 사람도 힘든 일이니..~~
// 오늘은 경제학에서 자주 사용되는 등탄력적 효용함수를 그려보도록 하겠습니다. 이때, 탄력도의 차이에 따른 함수 형태의 차이를 보고자 합니다.
// 그리고 탄력도의 차이에 따른 함수에 따라 소득수준에 따른 한계효용의 변화 역시 비교합니다.
// 등탄력적 효용함수의 일반적 형태...
// 이러한 효용함수의 특징은 소득수준에 따라 탄력도가 항상 ε로 같다는 것입니다.
// 즉, ε값에 따라 그 함수를 그리면 됩니다.
// 함수를 그리는 기본적인 코드는 다음과 같습니다.
twoway (function y = (x^(1-0) - 1)/(1-0), range(0 5)
// ε=0일때, x값 범위를 0과 5로하여 그래프를 그리시오....
// 즉, ε=0일때, 위 함수는 y=x-1이 됩니다...
// 이건 스타타 명령어 줄에서 아무런 자료가 없어도 그려집니다... 위의 function이라는 부분땜시...ㅋ
// 여하튼, ε가 0 , 0.5, 1, 2, 5일때 각 함수를 하나의 그래프로 그리려면....
#delimit ;
twoway (function y = (x^(1-0) - 1)/(1-0), ra(0 5) lcolor(black) lwidth(medium) lpattern(solid))
(function y = (x^(1-0.5) - 1)/(1-0.5), ra(0 5) lcolor(blue) lwidth(medium) lpattern(solid))
(function y = (x^(1-1.1) - 1)/(1-1.1), ra(0.07 5) lcolor(red) lwidth(medium) lpattern(solid))
(function y = (x^(1-2) - 1)/(1-2), ra(0.25 5) lcolor(green) lwidth(medium) lpattern(solid))
(function y = (x^(1-5) - 1)/(1-5), ra(0.52 5) lcolor(green) lwidth(medium) lpattern(dash))
, title("[등탄력도(ε)에 따른 효용함수]")
ytitle("효용(U)") yline(0, lstyle(foreground)) yscale(range(-3 4)) ylabel(-3(1)4, angle(horizontal))
xlabel(1(1)5, tposition(crossing)) xsca(noline)
xtitle("y/μ")
legend(on order(1 "ε=0" 2 "ε=0.5" 3 "ε=1" 4 "ε=2" 5 "ε=5") rows(1)) scheme(sj)
;
// 좀 복잡한가요? ㅠㅠ 어쨌든 그 결과는 다음과 같이 나름 괜찮죠!!
// 다음으로 위의 각 효용함수들에서 소득수준에 따른 한계효용의 궤적을 그리고 싶습니다.
// 이걸 그리기 위해선 일단 미분을 할 줄 알아야 하는데, 위의 효용함수를 미분하면 다음과 같습니다. 위의 함수보다 더 간단하죠~~
// 그러면 이제 위에 것도 이해했다면, 더 말할 것도 없습니다...ㅋ
twoway (function y = x^(-0), ra(0 5) lcolor(black) lwidth(medium) lpattern(solid))
(function y = x^(-0.5) , ra(0.057 5) lcolor(blue) lwidth(medium) lpattern(solid))
(function y = x^(-1) , ra(0.23 5) lcolor(red) lwidth(medium) lpattern(solid))
(function y = x^(-2) , ra(0.47 5) lcolor(green) lwidth(medium) lpattern(solid))
(function y = x^(-5) , ra(0.75 5) lcolor(green) lwidth(medium) lpattern(dash))
, title("[등탄력도(ε)에 따른 효용함수의 복지가중치 변화]")
ytitle("한계효용=복지가중치(ΔU)") yline(0, lstyle(foreground)) yscale(range(0 4)) ylabel(0(1)4, angle(horizontal))
xlabel(1(1)5, tposition(crossing)) xsca(noline)
xtitle("y/μ")
legend(on order(1 "ε=0" 2 "ε=0.5" 3 "ε=1" 4 "ε=2" 5 "ε=5") rows(1)) scheme(sj)
;
// 여하튼 오늘의 핵심은 twoway function문입니다.^^
// 아!! 이게 어떻게 쓰이는 함수냐구요?
// 분야마다 다르겠지만, 경제학에서 사용하는 불평등지수 중 앳킨슨 지수가 있는데, 위 함수는 그 지수를 산출하기 위한 가정한 함수입니다. 여기서 중요한 것은 ε 가 클수록 저소득계층의 한계효용값이 더 크게 나온다는 점입니다. 위의 그림에서 가로축은 평균소득 대비 개인소득의 비율이며, 그래서 1은 개인소득이 평균소득과 같다는 것입니다. 따라서 1보다 작은 부분이 저소득계층을 의미하는 것이고, 예를 들어 0.5의 경우 ε에 따른 한계효용을 비교하면, ε이 클수록 증가하고, 1을 초과하는 상위계층의 경우엔 ε을 크게 가정할수록 한계효용은 더 작게 됩니다. 이러한 한계효용값을 각 개인들의 소득에 대한 가중치로 설정하여, 평균이하 계층의 소득이 낮을수록 평균소득과의 격차가 더 크게 하여, 사회 전체적으로 각 개인들의 소득이 평균소득과 떨어진 거리를 표준화합니다. 표준화한 결과가 바로 앳킨슨 지수입니다.^^ 물론, 이 중간에는 넘 복잡한 수학적 풀이과정이 있어서, 더 자세한 설명을 드리지는 못하겠네요.... 쓰는 사람도 그렇고, 보든 사람도 힘든 일이니..~~


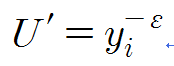



댓글
댓글 쓰기